Causal Vs Non Causal systems, Time variant and Time invariant, Linear Vs nonlinear system
Table of Contents
Causal VS Non Causal system:
We are discussing causal and non-causal systems together because they are closely related. We can easily differentiate between causal and non-causal systems. In order to find out if the given system is causal or non-causal we will check the relationship between output and inputs. In the first example the output Y (t) is equal to X (t) and you can see output Y (t) is dependent on the present input. So the system is producing a relationship in which the output is only dependent on the present input that’s why it is causal in nature because causal systems are those in which the output of system should not depend on or independent of future values of input and here the output of the system is independent of future values because it is only dependent on the present values.
Y (t) = x (t)
So we can define the causal systems in other way we can say causal systems are those systems in which the output of the system is only dependent on the present input or the output of the system is only dependent on the past input or the combination of both. It can either depend on present input past input or the combination of both the future values of input should not be there.
Y (t) = x (t) + x (t-1)
Where x (t) is present value and x (t-1) is past value.
So output YT is only dependent on the present and past values of input therefore this time also the system is causal in nature so I hope you know understand what our causal systems but there one more point is regarding the causal system which we must understand before moving to the non-causal systems. All real life systems or we can say all practical or physically realizable systems are causal systems.
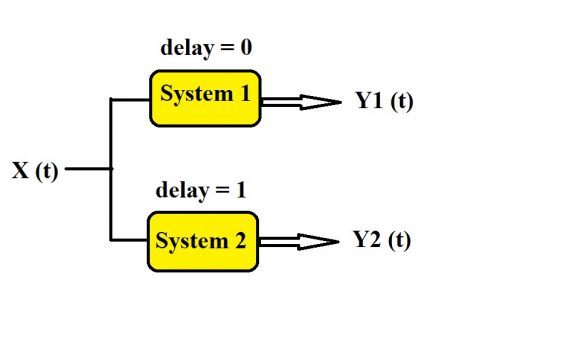
Let us take one example to understand this point in this example let us take two different systems the first system is system one and the second system is two and in both the systems the same input is given. Let’s say the input is X (t) and it is given to system number 1 and it is given to system number 2. The output of the first system is let’s say y1 (t) and the output of the second system is let say y2 (t). Now the difference between first system and the second system is the delay. In the first system the delay is equal to 0 and in the second system let us say the delay is equal to 1 this means in the first system when input x (t) is applied to system 1 the output y1 (t) is produced instantly on the other hand in the second system as delay is equal to one second when you apply input x (t) the output y2 (t) will be produced after one second. So this is the main difference between system 1 and system 2. We are focusing on how output is dependent on the input so what will happen when you provide signal x (t) to system 1 and system 2 at T equal to zero. In this scenario y1 (t) will be y1 (0) because t is equal to 0 and y1 (0) will be present value of output and it will depend on x (0) and y(0) because delay is equal to 0 and as soon as you provide the input when T is equal to 0 the output will be based on the same input you are providing at t equal to 0 and then input is x(0). So x(0) is the present value of input and you can see the present output is dependent on the present value of input so we can say that the output is only dependent on the present values of input and this will only possible when delay is equal to 0. So when delay 0 the output will depend on the present values of input so what is happening in system number one is very clear.
Now let’s move to system number two here delay is equal to one second and you are providing signal x (0) when t is equal to 0. The input signal is x (0) so output will be y2 (0) and will depend on x (t-1) because there is delay of 1 second and when T is equal to 0 actually the system is providing us the output which is based on this signal when T is equal to -1 second prior to 0 is T = -1. So we will have the output based on x (-1) when T is equal to 0. So the present value of output is dependent on the past values of input so this is the difference between system 1 and system 2 and all realized systems or practically realizable systems are having either this nature and in both the cases the output is not dependent on the future values of input. So we can see that causal systems are practical or physically realizable systems.
Now we will discuss what are non-causal systems. In non-causal systems the output of system is dependent on future values of input at any instant of time. So if there is at least one instant of time at which the output of the system is dependent on the future value of input the system will be non-causal. It may depend on past or present values but it should also depend on the future value at any one instant of time. This will be clearer when we will solve one or two examples based on it. In the first example signal:
Y (t) = x (t+2)
This is future value of input so the output is only dependent on the future value of input therefore the system is non-causal. Let’s take the second example in this example:
Y (t) = x (t) + x (t-1) + x (t+1)
Y (t) is dependent on the present past as well as future value of input therefore the system is non-causal in nature. So this is all for non-causal system. There is one more system known as anti-causal system. In case of anti-causal systems the property of system is entirely opposite of the property of causal system in causal system the output of system should be independent of the future values now what will be the exact anti or opposite of this statement. The output of the system should depend only on the future values of input. So the systems in which the output of the system is only dependent on the future values they are known as anti-causal systems for example if you see the first example here:
Y (t) = x (t+2)
The output of the system is only dependent on the future values of input there is no past or present value of input so this system is non-causal or it is anti-causal so anti causal systems.
Time variant and Time invariant:
This property makes the behaviour of system independent on time. A system is said to time invariant system if its input and output do not change with time. Every system that follows this property it behaviour will become independent on time.
If H {x (n)} = y (n)
Then H {x (n – k)} = y (n – k)
For every input signal x (n) and every time shift k.
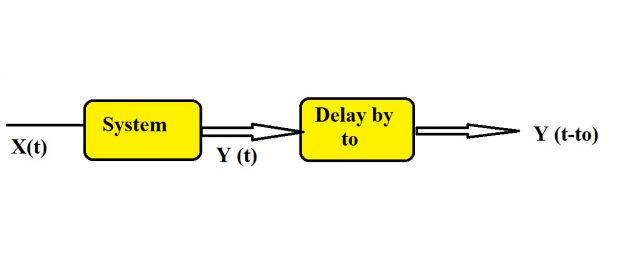
Time invariant and time variant property is important because we will also use it in LTI systems linear time invariant systems. Let us consider that X (t) will be the input to this system and we need to check if this system is time invariant or not. This system will give us output Y (t) but there is one change instead of directly recognizing this output Y (t). We will first provide a delay by t0 so we have another system and this system is providing a delay by t0 to the output of the first system. The original system whose property we are analysing. So Y (t) will become y (t-t0) after passing through the second system providing the delay by t0. So this is what we are doing in the first step.
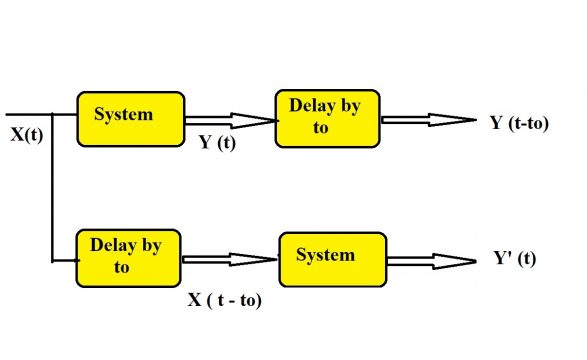
In the second step I want to switch the position of first system and the system providing the delay why because I want to provide the delay to the input itself instead of providing the delay to the output I want to provide the delay to the input itself and then I will pass it through the system and I will see if the two outputs are same or not.
So let’s see how we can do it you can see here the first system is the system providing a delay of t0 and the second system is the system under analysis. So what I will do I will provide the same input X (t) to the system providing the delay. So we have the connection like the same input X (t) is given to the system providing the delay. So the first output we will get will be x (t-t0).
The input was X (t) and we have provided the delay by t0. So we have x (t-t0) and now we will feed this x (t-t0) to the original system and we will have the output let’s say y’ (t).
Now there are two possibilities:
In the first possibility y ‘(t) may be equal to y (t-t0) and in the second possibility it may not be equal to y (t-t0). So let’s analyze the two situations in the first situation it is equal to y (t-t_0) and in the second situation it is not equal to y (t-t0) and when it is equal to y (t-t0) we call the system as time invariant system. Time when it is not equal to y (t-t0) we call it time variant system.
Linear VS Non-Linear system:
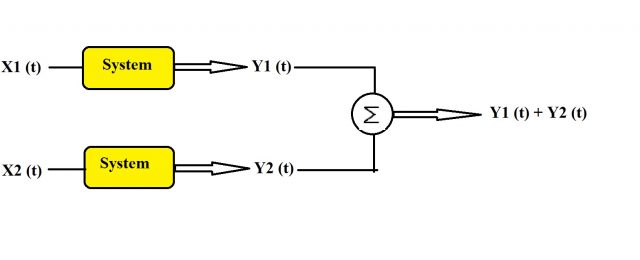
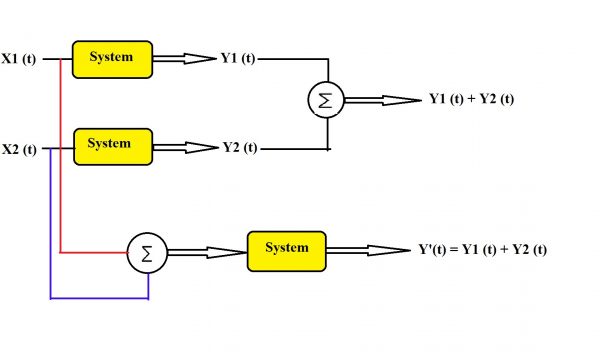
The system which follows the principle of superposition is known as linear system and the non-linear systems are those systems which do not follow the principle of superposition. So the important thing is to understand what is the principle of superposition? The principle of superposition or the law of superposition is sufficient and necessary condition to prove the linearity of the system so if you can prove the system is following the principle of superposition it is definitely going to be linear system because this particular principle is the necessary and sufficient condition. The principle of superposition is combination of two different laws the first law is known as law of additivity law of additivity and the second law is known as law of homogeneity. So we will first understand the law of additivity and once we are done with law of additivity we will understand law of homogeneity and the two laws combined will form the law of superposition. So let’s see what do we mean by the law of additivity? In order to understand the law of additivity let’s take one system and the input to this system is x1 (t) and the output of the system is y1 (t). So y1 (t) is the output obtained from this particular system when the input is x1 (t). Now we will change the input instead of having x1 (t) we will have a different input applied to the same system let’s say the input is x2 (t) and for this input the same system is generating the output y2 (t) so this is what we have and now we will add the two outputs y1 (t) and y2 (t) so this is what we will do in first step.
In second step instead of adding the outputs y1 (t) and y2 (t) we will add the two inputs x1 (t) and x2 (t). So the result of addition x1 (t) and x2 (t) will act as the input to the same system and the output generated we will compare with this result.
So let’s perform the addition of the two inputs first after adding the two inputs we will have:
Y’ (t) =x1 (t) + x2 (t)
Now there are two possibilities the first possibility is that the output Y’ (t) is same as y1 (t) + y2 (t) and the second possibility is that the output Y’ (t) is not same as y1 (t) + y2 (t). When the two results are same we see the system is following the law of additivity and in the second case when the two results are not same it is not following the law of additivity.
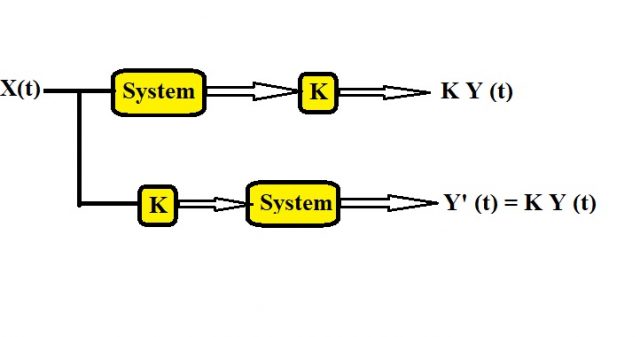
We can move on to check the law of homogeneity because the principle of superposition is composed of law of additivity and the law of homogeneity and if any one of these two laws are violated then the principle of superposition is violated and the system is nonlinear. So when you check the law of additivity and you find the two results are not same then stop right over there and you can write down the system is non-linear there is no need to check for the law of homogeneity because the law of additivity is violated and thus the principle of superposition is also violated and the system is non-linear. Now we will discuss what do we mean by law of homogeneity the law of homogeneity is a very simple law to understand it is very much similar to the law of additivity and as we are checking the linearity property of the given system we cannot change the system while checking if the system follows the law of homogeneity or not the system will remain same as it was in case of law of additivity. So we are having the same system and let’s say the input this time is x (t) and the output generated is Y (t). Now this time we will not perform any addition but we will perform the multiplication we will multiply a constant K to the obtained output Y (t) after multiplying K to the output Y (t). We will have K times y (t) so this is all we need to do in step number one. In step number two we will multiply the same constant to the input x (t) and the obtained result will act as the input to this system and then the generated output we will compare with KY (t) that’s why I was telling you law homogeneity is very much similar to the law of additivity. So let’s complete our step number two after multiplying k to X (t) we will have K x (t) and this K x (s) is the input to this system and the output generated.
Now again there are two possibilities y’ (t) may be equal to KY (t) or it may not be equal to KY (t). So in first possibility y’ (t) is equal to K Y (t) and in second possibility it is not equal to K Y (t). Now when y’ (t) is equal to KY’ (t) the first possibility we say the system is following the law of homogeneity and in case number 2 or the possibility number two when y’ (t) is not same as K Y (t). We say the system is not following the law of homogeneity. So this is all you should know about the law of homogeneity and there is no compulsion on checking the law of additivity first. You can check the law of homogeneity first and when you check the law for homogeneity first and you find the system is not following the law of homogeneity there is no need to check the law additivity because the system is going to be nonlinear as it has already violated the law of superposition.