Resistors in Series and Parallel, Solved examples, Basic electronics
Table of Contents
Resistors in Series and Parallel, Overview:
Resistors in Series and Parallel- When you start learning electronics, the very first electronic component you are introduced to is a Resistor. A resistor is passive two terminal electronic component which is used to limit the amount of current flowing through a circuit. Resistors are also used to step down the voltage, read my article on voltage divider. I have articles, in which I have explained,
What is a resistor, it’s types and applications
Carbon Resistor Vs Metal Film Resistor
Thermistor, a type of resistor
After, reading the above articles I am sure you will master the resistor. So, the very basic things I have already explained. In today’s article, I will only explain how to use resistors in series and parallel and then how to solve some basic circuits, to help you understand the basics. No, matter you are a student of engineering or B-tech, you will come across the Series and parallel circuits. Let’s first start with the Resistors in Series.
Resistors in Series:
So, today we will find the equivalent resistance when n number of resistors are connected in Series. Likewise, we will find an equivalent resistance when n number of resistors are connected in parallel combination. So, let’s start with the resistors which are connected in series combination.
So here, we have three resistors R1, R2, and R3, which are connected in series with one voltage source and the current flowing through the circuit is I. So, whenever the resistors are connected in the series combination, the same current will flow through each resistor. So here, the same current I will flow through resistors R1, R2, and R3. And because of flow the current, there will be drop across these resistors. So let’s say the drop is V1, V2, and V3. So now here we can apply Kirchhoff’s Voltage law. So applying KVL, we can write Vs- V1 – V2 – V3 = 0 Now, using the ohm’s law, we can write this V1 as I*R1, V2 as I*R2 and V3 as I*R3. So we can write Vs=I (R1+ R2 + R3). Let’s say this the equation number 1. Now, if we replace these three resistors by their equivalent resistance then the circuit will have one voltage source Vs, which is connected with an equivalent resistance. Let’s say that is Req and the current that is flowing through the circuit “I” will remain the same. So we can write, Vs as I*Req and let’s say this an equation number 2. Now comparing equation 1 and 2, we can write I*Req = I*(R1 + R2 +R3) that means Req = R1 + R2 +R3.
So we can say that if three resistors are connected in series then their equivalent resistance can be given as the sum of all the resistors. So, in general term, we can say that if n number of resistors are connected in series then their equivalent resistance can be given as summation of all the n resistors.
Resistors in Parallel:
Now, let’s see resistors which are connected in parallel combination. So here three resistors R1, R2, and R3 are connected in a parallel with one voltage source. Now, whenever the resistors are connected in a parallel combination, the voltage across each resistor remains the same. So here, the voltage across these resistors R1, R2 and R3 will be the same. That is voltage Vs. Let’s assume that the current supplied by this voltage source is “I”. So this current “I” will get divided into three branches. That is I1, I2, and I3. Where I1, I2, and I3 are the currents which are flowing through the resistors R1, R2, and R3. So, now here we can apply Kirchhoff’s current law. So applying KCL, we can write, I= I1 + I2 +I3 Now using the ohm’s law we can write I1 as Vs/R1, I2 as Vs/R2 and I3as Vs/R3. So we can write I= Vs*(( 1/R1)+ (1/R2) + (1/R3)) Let’s say this is the equation number 3. Now if we replace these three resistors which are connected in parallel, by their equivalent resistance then the circuit will have one voltage source Vs which is connected with an equivalent resistance. Let’s say that is Req. And the current that is supplied by the source will remain the same. So for this circuit, we can write I= Vs/Req Let’s say this is equation number 4. So comparing this two equations we can write, Vs/Req = Vs* (1/R1 + 1/R2 + 1/R3) So we can write 1/Req = (1/R1) + (1/R2) + (1/R3) So in this way, if three resistors are connected in parallel then their equivalent resistance can be given by this expression
So in a general way, we can say that, if n numbers of resistors are connected in parallel then their equivalent resistance can be given by this expression.
Resistors in Series and Parallel:
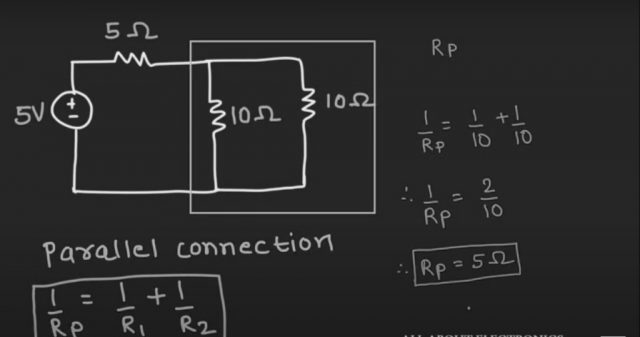
So, now let’s take one example based on the series and parallel combination of the resistors. So here we have given one circuit. And in this circuit, we need to find a current “I” that is supplied by this voltage source. So, in this circuit, we are not bothered about the voltage or current across any of the resistors. So simply we can replace all the resistors by their equivalent resistance and using the ohm’s law we can find this current “I”. So, these two 5 ohm resistors are connected in a series combination. So we can replace these two resistors by their equivalent resistance. So let’s say their equivalent resistance is Rs. So Rs can be given as 5 + 5, that is 10 ohm.
So, now the circuit will look like this. So, now in this equivalent circuit, if you see, these two 10 ohm resistors are connected in parallel.
So, we can replace these two resistors by their equivalent parallel resistance. So let’s say their equivalent parallel resistance is Rp and Rp can be given by this formula. So, we can write, 1/Rp = 1/10 + 1/10 that means 1/Rp = 2/10 that is nothing but Rp = 5 ohm So, now the circuit will have two 5 ohm resistors which are connected in a series.
Let’s say their equivalent series resistance is Rs’. That is nothing but a summation of these two resistors. That is 10 ohm. So, now circuit has one 5 V voltage source, which is connected with a 10 ohm equivalent resistance. And the current I, can be given as I = V/ R. That is nothing but 5/10. That means I = 0.5 A. So, I hope you understood how to find the equivalent resistance when a bunch of resistors are connected either in series or in parallel combination.
So, we are done with the very basic series and parallel circuits, but the circuits are not as simple. There are so many complicated circuits in which the resistors are connected in different branches and needs special consideration and knowledge to solve such complex circuits. Take a look at the following circuit. Even though this is not a complex circuit but quite different from the one’s we just solved. Now this circuit is a step towards solving complex circuits. So from now on we will be solving some intermediate level and complex level resistor circuits, that I am sure will help you in exams.
So, notice that these three resistors (5ohm, 3ohm, and 2ohm) are in series with each other and so the equivalent resistance of those three is going to be 5 + 3 + 2 which is 10. So, we can replace those three resistors with a single 10 ohm resistor. Now every other part of the circuit is going to remain the same. Initially, so this is 10 ohms and this is still 10 this is still 5 and that’s still 10 ohm.
Now, notice that we have two resistors in parallel they’re directly across from each other and they have the same resistance. Whenever you have two parallel resistors with the same value the equivalent resistance is simply half of that value so individually they’re both 10. So, the equivalent resistance is going to be 5. So, we can get rid of this and replace it with a 5 ohm resistor.
So, now these three are in series with each other. so then we could just add them 10 + 5 + 5 is 20. So the equivalent resistance in the circuit is 20 ohms.
Once you have the equivalent resistance, you could find the current that is delivered from the battery and you could use V = IR. So if you rearrange this equation to solve for I the current is gonna be the voltage of the battery divided by the total resistance or the equivalent resistance. So the voltage of the battery is 60 volts in this example and the equivalent resistance is 20 ohms, so 60 divided by 20 is 3 amps so that’s the current that leaves the battery.
Now let’s call this position a and let’s say this is b c d e and f. Now, in order to calculate the current that’s flowing through each resistor it’s helpful to know the potential at each of these points and we’re gonna say at Point a the potential is zero volts. So, now if we travel in this direction from A to B we’re going towards the positive terminal of the battery and the battery increases the energy of the circuit because it delivers power to the circuit. So, as we go from A to B, so the potential at B is 60 volts. Now something else you need to know is that whenever or current flows through a resistor the current flows from a high potential to a low potential, so we have the current of 3 amps its flowing through the 10 ohm resistor so let’s call that just reamp so that means this is positive and this is negative. so see is that a lower potential than B so to calculate the potential, it’s going to be the potential at B minus IR because C is lower than B so the potential at B is 60 volts the current flown through the 10 ohm resistor is 3 amps multiplied by 10, so 3 X 10 is a voltage drop of 30 and then 60 minus 30 tells us that the potential at C is 30 volts. Now let’s go from A to F. now this 3 amp current which flows through the battery also flows to the 5 ohm resistor because this path here they’re all in serious whenever there’s only a single path for the current to flow you have a series path and the current flowing through that path is the same everywhere along that path. so what this tells us is that 3 amps of current flows through the 5 ohm resistor and current always flows from a high potential to a low potential. So as we travel from A to F that’s going to be a voltage lift because we’re going from the negative side to the positive side. So anytime you go against the current the electric potential is increasing if you’re following the current like we did over here the potential decreased. So to calculate the potential at F is going to be the potential at a plus IR because we’re going towards a higher potential. So this is gonna be plus instead of minus so the potential at any is zero the current flowing through the five ohm resistors three amps times five so the potential at F is going to be fifteen volts.
Now let’s get rid of this and let’s focus on the 10 ohm resistor because we now have the potential across C and across F so we can calculate the current flowing through that resistor. Now voltage is equal to current times existence based on Ohm’s law and voltage is also known as the potential difference between two points so we know that the current is flowing in this direction and also current flows from a high potential to a low potential. So the potential at C is higher than the potential at F so the voltage across that resistor is going to be the potential at C minus the potential at F and that’s equal to the current times the resistance so the potential at C is 30 the potential at F is 15 and we don’t know the current yet but the resistance is 10 so 30 minus 15 will give us a voltage of 15 volts across that resistor and so 15 divided by 10 is 1.5 so that’s the current that flows through the 5 ohm resistor.
So now we could calculate the current that flows through the other branch so let’s focus on Junction C at that Junction we have a current of 3 amps that is entering the junction and 1.5 amps flows in this direction now according to Kirchhoff’s current law junctionville the total current that enters into a junction is equal to the total current that leaves the junction so if we call this I 1 and this I 2 then this must be I 3 and so I 1 enters the junction and the other two currents they leave it so i1 is equal to i2 plus i3 so i1 is three amps I 2 is 1.5 so I 3 is 3 minus 1.5 so this is also 1.5 amps so now we have the current flowing through the remaining three resistors so I’m just gonna put it here 1.5 amps.
Now since the current flows from C to D you know this is gonna be positive and this is negative and it flows from D to E, so E is at low potential then D, then it flows from E to F which means E is at a higher potential than F. now let’s calculate the electric potential at point D so the potential at Point D is going to be the potential at Point C minus IR because as we go in the direction of the current we’re going towards a lower potential. So D is lower than C, the potential at C is 30 the current flowing through the 5 ohm resistor is 1.5. So the voltage drop is 1.5 times 5 which is 7.5 and so 30 minus 7.5 tells us that the potential at D is 22.5 volts now let’s calculate the potential at E. So we have another voltage drop because we’re going towards a lower potential as we follow the direction of the current. So it’s gonna be VD minus IR so the potential at D is 22.5. We still have a current of 1.5 but this time it goes to a 3 ohm resistor. So 3 X 1.5 that’s a voltage drop of 4.5 then 22.5 minus 4.5 gives us a potential of 18 volts at E now to confirm the answer, let’s calculate the current going through the 2 ohm resistor.
We already know it’s 1.5 but let’s confirm that answer, because we have the potential at Point F so the potential at E minus the potential at F represents the voltage across the 2 ohm resistor and voltage is equal to current times resistance. So, the potential at E is 18 the potential at F is 15 and R is 2. So, 18 – 15 gives us a voltage of 3 volts and so 3 divided by 2 is 1.5 which is in agreement with this answer. So now we’ve completely solved the circuit. We’ve calculated the current flown through every resistor and we also know the electric potential at every point in a circuit and so that’s it now if we wish to calculate the power absorbed by resistor.
Let’s say if we want to calculate the power absorbed by this resistor we can use this formula I squared x R. So, the current that’s flowing through it is 1.5 and the resistance is 10, so the power absorbed by that resistor is simply 22.5watts. Now if we wish to calculate the power delivered by the battery we can use this formula its voltage x current. So, we have 60 volts times the current of three amps and so that’s gonna be 180watts. Now the power delivered by the battery must be equal to the power absorbed by each resistor and that’s the second way you can confirm if you have the right answer. So let’s calculate the power absorbed by each resistor so we already have this one and we said that’s 22.5 watts. Now, let’s focus on this resistor so it’s I2 R. it’s 3 squared times 10 and so the power absorbed by that resistor is 90 watts and for this one I2 R it’s gonna be 32 x 5 and so it’s 45 watts for that resistor and now for this one it’s gonna be 1.52 x 5 and that’s 11.25 and then for this one it’s a 1.52 x 3 and so that’s only 6.75 and then for this one 1.52 x 2 so that consumes 4.5 watts.
So, now let’s add up all the numbers so we have 90 watts + 45 + 22.5 + 11.25 + 6.75 + 4.5. let’s see if that adds up to 180 and indeed it does. So the total power absorbed by the resistors is equal to the power delivered by the battery. So for this circuit the values that we just calculated are correct.
Now let’s work on a similar circuit but one that’s slightly different in the way so we’re just going to add one more resistor to the circuit that we had before and the values will change of course. So what if we put a resistor right in the middle so this time we’re gonna have a 120 volt battery and this resistor is gonna be 10 ohms and this one is 12 ohms and this is going to be an 8 ohm resistor and then 3, 9, 5 and in the middle this is gonna be a 4 ohm resistor. So, what you can do stop over here and calculate the current that is delivered from the battery and the current that flows through each resistor in a circuit so go ahead and try this. The calculated values are given below.