Kirchhoff’s Laws, Kirchhoff’s Voltage Law & Kirchhoff’s Current Law
Table of Contents
Introduction:
Kirchhoff’s Laws: these laws are use to find the current in different branches of an electrical network which may be easily solved by ohms law, Kirchhoff’s laws are two in number
- Kirchhoff’s first law or Kirchhoff’s current law “KCL”
- Kirchhoff’s loop law or Kirchhoff’s voltage law or Kirchhoff’s mesh law “KVL”.
Kirchhoff’s laws are applicable to both Ac and Dc.
-
Kirchhoff’s current Law
Kirchhoff’s current Law this law states in any electrical network that
“The algebraic sum of current meeting at a junction or node or point is zero”
Or
In other words “the sum of currents flowing towards the junction is equal to the sum of the currents flowing away from the junction”.
Let we consider the arrangement of 4-wires connected together at point “0” as shown in fig below.
The arrows indicate the direction of flow of current. The currents I1 and I4 are coming towards the junction and current I2 and I3 are going out from junction we assume (suppose ) +ive sign for incoming current and –ive sign for outgoing current. Now according to the Kirchhoff’s Current Law “KCL”
∑I=0
Now from fig
I1+I4+(-I2)+(-I3)=0
I1+I4-I2-I3=0
I1+I4=I2+I3
Or incoming currents = outgoing currents
Problem1:
Determine the currents I3 and I4 for the giving circuit using Kirchhoff’s Current Law “KCL”.
Solution:
At point a by Kirchhoff’s
∑ Iincoming = ∑ Ioutgoing
I1+I2=I3
2+3=I3
= I3 = 5
At point “b” by Kirchhoff’s law
∑ Iincoming = ∑Ioutgoing
I3 + I5 =I4
5 +1=I4
I4=6amp
Problem2:
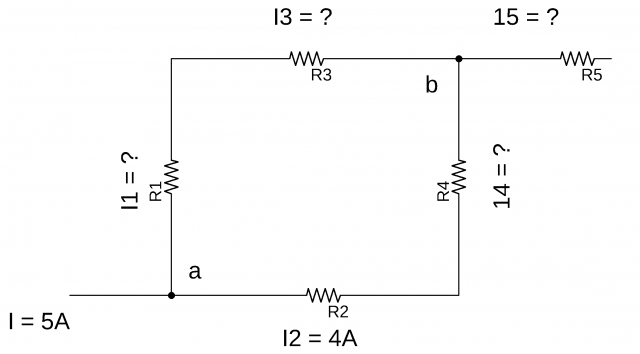
Find I1, I3, I4, and I5 in the network given
Solution:
At point a
I= I1+I2
5=I1+4
5-4=I1
I1=1amp
As R1 and R3 are connected in series and we know that in series same current will pass through each resistor so
I3=1amp
And we know that R2 and R4 are connected in series so, current will be same therefore
I4=4amp
As I5 = I4 + I3
I5 =4+1
I5=5amp
Problem3:
Find the magnitude and direction of I3 and I4
I6 and I7 for the network using Kirchhoff’s Current Law KCL.
Solution:
Incoming current I1= 10amp
Outgoing current I7=10amp
At point b we see that
I2 = I4 +I5
I2 = I4 +8
4= I4
As at point d we see that
I7 = I5 + I6
10 =8 +I6
10-8 = I6
I6 =2amp
As at c point we see
I6 + I3 = I4
2 +I3 = 4
I3 = 2amp
-
Kirchhoff’s Voltage Law:
This law states that “the algebraic sum of all the voltage taken in a specified direction taken around the closed loop is zero”.
Mathematically
∑v=0
Closed loop:
A closed loop or a closed path is any continuous path that reaches a point in one direction and return to the same point from another direction without leaving the circuit.
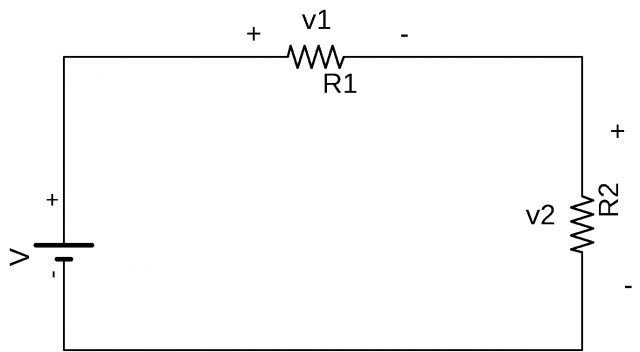
Consider the circuit
Apply Kirchhoff’s Voltage Law KVL to the circuit we have
∑v=0
-(xR1) + (-v1)- R2(-z)+ v2 –R3(-y)
-xR1-v1+R2z+v2+R3y=0
For conformity the clock wise direction will be closed throughout all application of Kirchhoff’s Voltage Law KVL also anti clock wise direction can be used and both will gives us the same result.
Problem1:
Write the voltage equation for the given circuit
Solution:
-v1-v2+v=0
V=v1+v2
∑vrise =∑vdrop
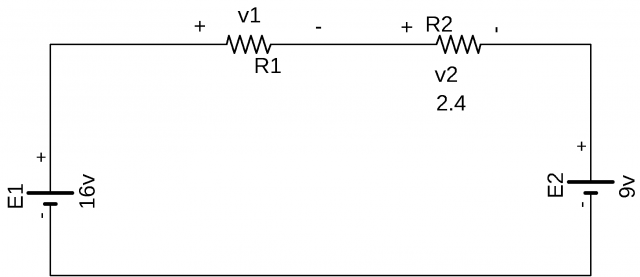
Problem2:
Find the voltage v1 for the network shown
Solution:
-v1-v2–∈2+∈1=0
Putting values
-v1 -4.2-9+16=0
V1= -4.2-9-16
V1=16-13.2
V1=2.8vout