Power Factor Improvement, Power Factor calculation Inductive and Capacitive loads
Table of Contents
Power factor:
Power factor is the ratio of true power divided by the total power or apparent power. First we will understand what true power is:
True power:
We use the true power through substation using the distribution lines and we are using this power to power up our appliances. Now this true power is the actual power which is being utilized for doing some useful work by the appliance. In case of electric fan the true power is the power which is being utilized to run this fan or to say it is the power which is being required to rotate the wings of this fan. The true power is the friction of the total power which is being supplied to this device. So apart from the true power, we also have reactive power.
Reactive Power:
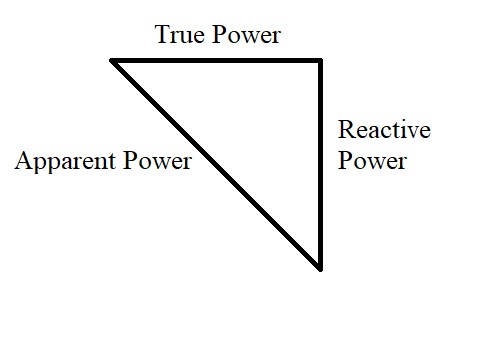
So as its name suggest the reactive power is being utilized in the reactive of element of the load. In case of this fan this reactive power is utilized in generating the magnetic field inside the motor of this fan. So this reactive power does not contribute in generating some useful work but still it is required to generate the magnetic flux so that the motor of the fan can be rotated. So in this way we have total two components the true power and the reactive power. The vector sum of this true power and the reactive power is known as apparent power.
Generally the true power is represented by the symbol P and the reactive power is denoted by the symbol Q and this apparent is denoted by the symbol S. So now let us consider about these different powers and the power factor by taking one circuit example.
Consider a single phase 230V ac supply to which a purely 60 ohms resistor load is connected to find current flowing through this system.
We will divide the voltage by the resistance:
V=IR
I=V/R
I=230/60
I=3.83 A
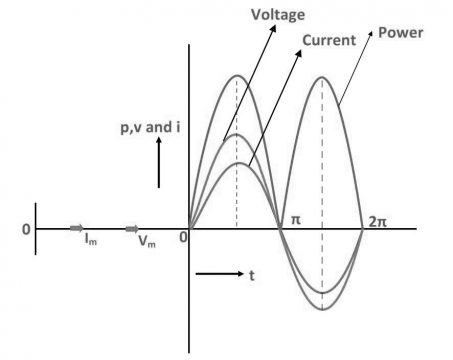
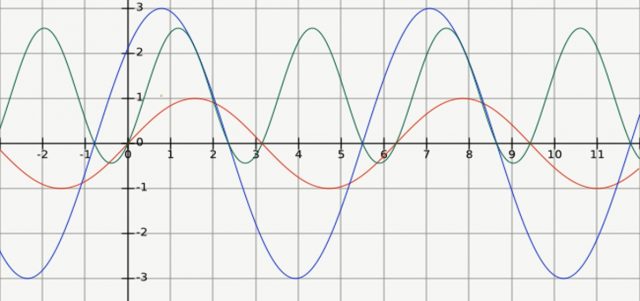
As this is resistive circuit the current and voltage will be in phase with each other. In phase means the current and voltage reaches their zero value and their peak value at the same time. Now if we draw power waveform of this circuit it will look like
The power will be always positive which means that whatever power is taken by the system is being utilized and no power is wasted.
P=VI
P=230×3.83
P=880.9 watt
The 880.9 watt power is produce by the source generator it would only take mechanical energy and we can say that power taken by this circuit is active power.
Case 2:
Now we will replace 60 ohm resistor with 160 milli Henry inductor to calculate current flowing through this circuit.
We first need to calculate the reactance of the inductor and we can do that by using the formula:
XL=2πfL
XL=2π×50×0.16
XL=50.24 ohms
Now we can calculate the current in the circuit:
V=IR
I=V/R
I=230/50.24
I=4.57A
As this is purely inductive circuit current is out of phase with voltage by 90 degree to get power of this circuit we will multiply voltage and current at every instance and the resultant power waveform in such circuit the power will be alternating between positive and negative value. This means that some amount of power is taken by the circuit and the same amount is return and the power is called reactive power.
P=VI
P=230×4.571
P=1051.1 VAR
Case 3:
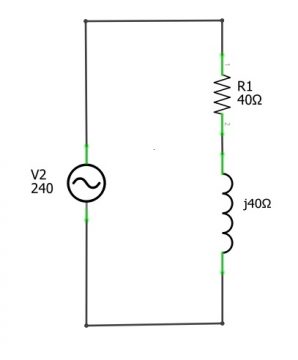
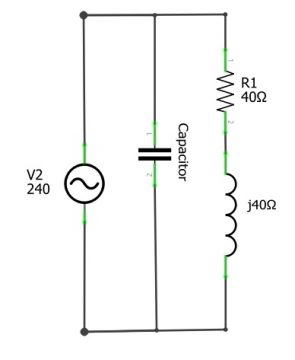
Now if we add inductor with resistor. Let us consider the value of resistor is 40 ohm and the value of the reactance of the inductor is j40 ohm.
So the current “I” which is being drawn from the source will be equal to:
I= 240/(j40+40)
I= 4.2426<-45
Now if we see the waveform of voltage and current. The voltage will lead the current by 45 degree and when we multiply these two waveforms; it will shows us that for most of the time power is being absorbed from the source but for the small portion of time the power is getting supply back to the source and that is because of the reactive element in our circuit. So first we will find the true power as well as the reactive power. So the true power will be equal to:
P=I2 R
P=(4.2426)2×40
P=720 watt
Now the reactive power can be find by using the formula:
Q=IXL
P=(4.2426)2×40
P=720 watt
So in this way we can get both true and reactive power. Now we will find the total power or apparent power by simply multiplying the voltage and current:
S=4.2426×240
S=1018 VA
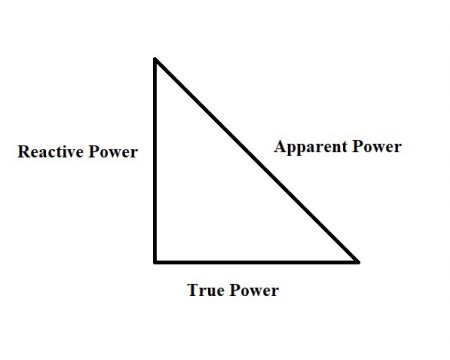
Now we will represent these powers in phasor diagram then using the power
S=√(P2+Q2 )
This power triangle is very similar to the impedance triangle of a series RL circuit. So in case of the series RL circuit if we see the impedance triangle:
The angle is Φ so we can write angle as:
cosΦ =R/Z
Whenever we multiply all the three side with the I^2 this impedance triangle will be converted into power triangle. So the ratio of the true power and apparent power will give us the power factor.
cosΦ =(I2 R)/(I2 Z)
cosΦ = P/S
The power factor can also be represented bycosΦ . The reactive element is purely inductive but if we have capacitive reactance then the power triangle will look like:
So in any case the power factor will be equal to cosΦ whether the load is inductive or capacitive the value of the power factor will be in the range of -1 to 1.
Inductive load:
So whenever we have inductive load the value of the power factor will be between 0 and 1. In inductive load the power factor is known as lagging power factor because in inductive load the current lags the voltage.
Capacitive load:
Whenever we have a capacitive load the value of the power factor is between -1 and 0. In capacitive load the power factor is known as
leading power factor because in capacitive load the current lead the voltage.
The power factor of the resistive and inductive load circuit can be calculated by:
As we calculate above that true power is equal to 720 watt and the apparent power is equal to 1018 VA.
Power factor = P/S
Power factor = 720/1018
Power factor = 0.707
The value of the power factor should be closed to the unity. So when we have poor power factor it means that we are drawing theadditional power for the reactive element across the load and this additional power means we are drawing the additional amount of the current which will introduce the voltage drop across the cables that means we will receive less amount of the voltage at our homes and offices. So all these thing are basically additional amount of burden on the power supplier. So whenever we have poor power factor then these power suppliers used to charge for the poor power factor which is known as the power factor penalty. So when we have poor power factor the electricity bill of our system will also increase. So that is the reason in the industry the most importance is given to the power factor.
Power factor Improvement:
Now let us consider that we have inductive load which consist of resistor as well as inductor and we consider that the power factor for this system is cosΦ1 . So to improve the power factor we will reduce the angle and when this angle is zero we have unity power factor. So reduce the angle we need to reduce the value of the reactance so when we introduce capacitor in the circuit. The capacitive reactance will be subtracted from the inductive reactance and because of that the effective reactance will be reduced and so the power factor will be improved. Let us consider that by introducing the capacitor our factor will be cosΦ2 and the new reactance will be X. Where X is equal to:
X= XL-Xc
Xc = XL– X
Xc = XL– X
Xc=R[tanΦ1-tanΦ2]
So if we know the value of initial power factor and the improved power factor then we can calculate the value of this capacitive reactance from the above circuit we know that the power factor value is 0.707 and we want to improve this power factor to the unity then the value of the reactance should be equal to zero that means the capacitive reactance should be to this inductive reactance. Now we know that the reactive power will be equal to:
Q= V2/XL = V2/XC
XC = V2/Q
XC = 2402/720
So from these calculations we get the value of Xc
Now to find the value of the capacitor we will use the formula:
Xc=2πfC
C=Xc/2πf
C=80/(2π×50)
C=40µF
So by just introducing 40µF capacitor we can achieve unity power factor in our circuit. By introducing this capacitor the total power will also be reduced. So for this we need to find the overall impedance of the circuit which is:
Z=Xc|| ZL
The impedance of the capacitor is –j80
Z=(-j80×(40+j40))/(40-j40)
When we calculate the value we get the Z value:
Z=80 ohm
Now to calculate the amount of the current that can be drawn from the source is:
I=240/80
I=3A
Now we can see that earlier the circuit draw 4.2426 ampere current while now it can draw 3A current. The power factor of the circuit will be equal to one.
These calculations are for the linear loads which include capacitor, resistor and inductor. But in actual system if we see we have non-linear loads like in case of the variable frequency drive or servo drives we use to have Rectifier Bridge or rectifier circuits inside these drives so because of these non-linear elements we have the harmonics of the current. That means apart from the fundamental frequency of the current we also used to have harmonics and because of these harmonics the distortion of the current occur and we have degradation in the power factor.
Displacement Power factor:
Whenever we have linear loads then the power factor is known as displacement power factor because the degradation in the power factor will be due to the reactive element present in the circuit. Because this reactive element introduces phase difference between the voltage and current so this type of power factor is known as displacement power factor.
Distortion power factor:
When we have a non-linear load then in such case we also used to get harmonics of the current that is the distortion in the waveform. So because of this whatever degradation that we used to get in the power factor is known as distortion power factor. In actual system we have both type of power factors.
Total power factor= displacement PF × distortion PF
So in the practical system when we have non-linear loads then in such case just by applying the capacitor we cannot improve the power factor because this degradation the power factor is because of the harmonic distortion. So for that we first of all remove these harmonics of the current that can be achieved by applying the passive or the active harmonic filters. So in this way when we have a non linear load then by applying the passive or active harmonic filter we can improve the power factor of the system.
Why to improve power factor?
Let us consider that we are building a steel plant for which we have brought 200 KVA transformer which is capable to transfer 170 KW of power. Similarly we also brought 1 Horse power induction motor and other required equipment. Based on calculation we found that the current is 280 Ampere RMS. We find that the power factor of our system is 0.707. As we are using 220 KVA transformer which will give 170 KW power; as the power factor of the system is 0.707 then the power will be:
0.707 × 220 = 140 KW
So this is the first reason due to which we increase the power factor. If we improve the power factor to 0.9 then the transformer will deliver 180 KW power.
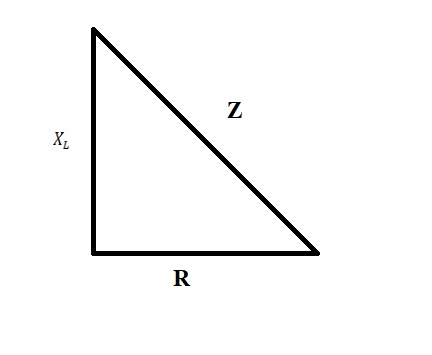




A very good website I would like to visit again