Selection Sort Algorithm in C / C++ With Program Examples
Table of Contents
What is the Selection Sort :
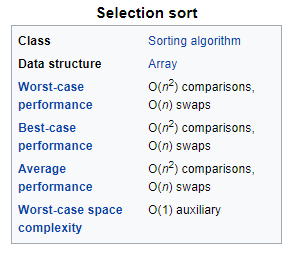
In computer science, selection sort is an in-place comparison sorting algorithm. It has an O(n2) time complexity, which makes it inefficient on large lists, and generally performs worse than the similar insertion sort. Selection sort is noted for its simplicity and has performance advantages over more complicated algorithms in certain situations, particularly where auxiliary memory is limited.
The algorithm divides the input list into two parts: a sorted sublist of items which is built up from left to right at the front (left) of the list and a sublist of the remaining unsorted items that occupy the rest of the list. Initially, the sorted sublist is empty and the unsorted sublist is the entire input list. The algorithm proceeds by finding the smallest (or largest, depending on sorting order) element in the unsorted sublist, exchanging (swapping) it with the leftmost unsorted element (putting it in sorted order), and moving the sublist boundaries one element to the right.
The time efficiency of selection sort is quadratic, so there are a number of sorting techniques which have better time complexity than selection sorting. One thing which distinguishes selection sort from other sorting algorithms is that it makes the minimum possible number of swaps, n − 1 in the worst case.
Amazon Purchase Links:
*Please Note: These are affiliate links. I may make a commission if you buy the components through these links. I would appreciate your support in this way!
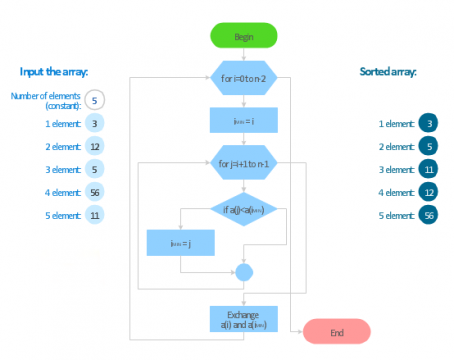
Selection Sort Flow Chart:
The selection sort method is also used for sorting arrays in ascending or in descending order. If an array has n elements, n-1iterations are required to sort the array.
The selection sort method is used to sort an array in ascending order.
In the first iteration, the value in the first element is assumed to be the 3 smallest. Then the next smallest element is found in the array. This value is interchanged with the first element. Now the first element of the array has the smallest value.
In the second iteration, the smallest value from the second element to the last element of list is found. This value is interchanged with the second element of the array.
This process is repeated until the entire array is sorted.
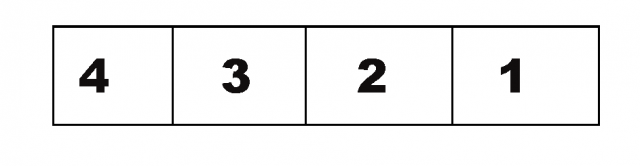
In the following example. The array that has 4 elements is sorted by selection sorting. There will be also three iterations to sorting the list in ascending order with the selection sorting method.
The array is :
Sorting Iterations:
Selection Sort first Iteration:
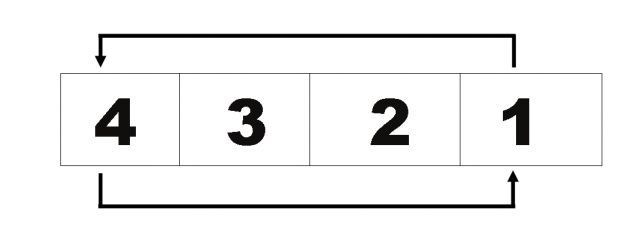
find out the smallest value from the list starting from the first element to the last element of the list. The smallest value is 1 in location 4. Note this address of the element that has the smallest value. interchange the value of the first element with the fourth element. Ie swap values or data[0] and data[3].
Selection Sort Second Iteration:
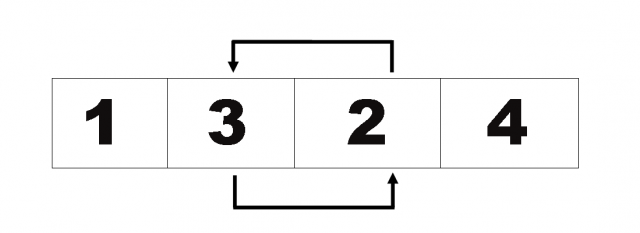
find out the smallest value from the list starting from the second element to the last element of the list. The smallest value is 2 in location 3. Note this address of the element that has the smallest value. interchange the value of the second element with the third element. Ie swap values or data[1] and data[2].
Selection Sort third Iteration:
find out the smallest value from the list starting from the third element to the last element of the list. The smallest value is 3 in location 3. Note this address of the element that has the smallest value. as you can see that 3 is less than 4 which is the last fourth element in the list and here It cannot interchange the value with the fourth element with the third element. Because the array is already in sorted form. So in this way, a selection sorts works
Example write a program which sorts the data in ascending order using the selection sort algorithm in c++:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
#include<iostream.h> #include<conio.h> main() { int i, u, p, m, t, data[4]={4,3,2,1}; clrscr(); for(u=0; u<3; u++) { m=data[u]; for(i=u; i<=3; i++) if(m> data[i]) { m=data[i]; p=i; } t=data[p]; data[p]=data[u]; data[u]=t; } cout<<”value is sorted”<<endl; for(i=0; i<=3; i++) cout<<data[i]<<endl; } |